HOME work papers html 2009fermi

B.1 Mathematical description of the method

The method adopted by most algorithms to reduce a matrix A to a diagonal form is to apply a sequence of similarity transformations:

$\displaystyle A \rightarrow P_1^{-1} \cdot A \cdot P_1 \rightarrow P_2^{-1}\cdot P_1^{-1} \cdot A \cdot P_1 \cdot P_2 \rightarrow$ etc.

(B.1)

So that eventually we have:

$\displaystyle D$	$\displaystyle =$	$\displaystyle R \cdot A \cdot R^{-1}$	(B.2)
$\displaystyle R$	$\displaystyle =$	$\displaystyle P_1 \cdot P_2 \cdot \dots$	(B.3)

For the Jacobi method, these transformations consists of orthogonal similarities. Each Jacobi transformation, is a plane rotation designed to annihilate one of the off-diagonal matrix elements. Successive transformations undo previously set zeros, but the off-diagonal elements nevertheless get smaller and smaller, until the matrix can be considered diagonal for a given precision. Moreover the product of the transformations,

in equation B.3, is the matrix of eigenvectors. The Jacobi method is absolutely foolproof for all real symmetric matrices. For matrices of order greater than about 10, the algorithm become slower than other algorithms. However, the Jacobi algorithm is much simpler than the more efficient methods.

The basic Jacobi rotation $P_{pq}$ is a matrix of the form

$\displaystyle P_{pq}= \left[ \begin{array}{ccccccc} 1 & & & & & &\\ &\dots & & ... ...s& & &\\ & & -s& &c & &\\ & & & & & \dots&\\ & & & & & &1\\ \end{array} \right]$

(B.4)

The numbers and are the cosine and sine of a rotation angle $\phi$ :

$\displaystyle c = \cos(\phi) \ ; \ s = \sin(\phi)$

(B.5)

The Jacobi rotation is used to transform matrix with the similarity:

$\displaystyle A' = P_{pq}^{T} \cdot A \cdot P_{pq}$

(B.6)

Now, $P_{pq}^T \cdot A$ changes only rows and of , while $A \cdot P_{pq}$ changes only its columns and . The result of the product on each side is, for $r \neq p, r \neq q$ :

$\displaystyle a'_{rp}$	$\displaystyle =$	$\displaystyle ca_{rp} - sa_{rq}$	(B.7)
$\displaystyle a'_{rq}$	$\displaystyle =$	$\displaystyle ca_{rq} + sa_{rp}$	(B.8)

and otherwise:

$\displaystyle a'_{pp}$	$\displaystyle =$	$\displaystyle c^2 a_{pp} + s^2 a_{qq} - 2sca_{pq}$	(B.9)
$\displaystyle a'_{qq}$	$\displaystyle =$	$\displaystyle s^2 a_{pp} + c^2 a_{qq} + 2sca_{pq}$	(B.10)
$\displaystyle a'_{pq}$	$\displaystyle =$	$\displaystyle \left(c^2 - s^2 \right) a_{pq} + sc\left(a_{pp} - a_{qq} \right)$	(B.11)

Let's remember that we want to try to annihilate the off-diagonal elements. and are similar, so they have the same Frobenius norm $\vert\vert.\vert\vert _F$ : the sum of squares of all components. However we can choose $\phi$ such that $a'_{pq} = 0$ , in which case has a larger sum of squares on the diagonal. As we will further see, this is important for the convergence of the method. In order to optimize this effect, $a_{pq}$ should be the largest off-diagonal component, called the pivot. From equation B.11, $a'_{pq} = 0$ yields:

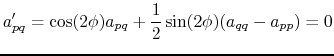$\displaystyle a'_{pq} = \cos(2\phi) a_{pq} + \frac{1}{2} \sin(2\phi) (a_{qq} - a_{pp}) =0$

(B.12)

from which we define $\theta$ :

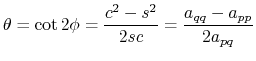$\displaystyle \theta = \cot 2\phi = \frac{c^2 - s^2}{2sc} = \frac{a_{qq} - a_{pp}}{2a_{pq}}$

(B.13)

If we let , the definition of $\theta$ can be rewritten

$\displaystyle t^2 + 2t\theta - 1 = 0$

(B.14)

We choose the smaller root of this equation, where the rotation angle is less than $\pi/4$ . This choice gives the most stable reduction. The smaller root is:

$\displaystyle t= \frac{\text{sgn}(\theta) }{\vert\theta\vert + \sqrt{\theta^2 + 1}}$

(B.15)

If $\theta$ is so large that $\theta^2$ would overflow on the computer, we set $t = 1/(2\theta)$ . It now follows that

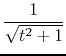$\displaystyle c$	$\displaystyle =$	$\displaystyle \frac{1}{\sqrt{t^2 + 1}}$	(B.16)
$\displaystyle s$	$\displaystyle =$	$\displaystyle tc$	(B.17)

To minimize numerical roundoff error, equation B.11 is replaced by $a'_{pq} = 0$ The idea in the remaining equations B.7 - B.11 is to set the new quantity equal to the old quantity plus a small correction. Thus we can use $a'_{pq} = 0$ to eliminate $a_{qq}$ from B.9, giving

$\displaystyle a'_{pp} = a_{pp} - ta_{pq}$

(B.18)

Similarly,

$\displaystyle a'_{qq}$	$\displaystyle =$	$\displaystyle a_{qq} + ta_{pq}$	(B.19)
$\displaystyle a'_{rp}$	$\displaystyle =$	$\displaystyle a_{rp} - s(a_{rq} + \tau a_{rp} )$	(B.20)
$\displaystyle a'_{rq}$	$\displaystyle =$	$\displaystyle a_{rq} + s(a_{rp} - \tau a_{rq} )$	(B.21)

where $\tau (= \tan \phi/2)$ is defined as

$\displaystyle \tau=\frac{s}{1+c}$

(B.22)

One can see the convergence of the Jacobi method by considering the sum of the squares of the off-diagonal elements:

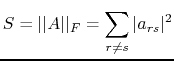$\displaystyle S=\vert\vert A\vert\vert _F=\sum_{r \neq s }\vert a_{rs}\vert^2$

(B.23)

Using equations B.7 - B.11 and the similarity properties, we have:

$\displaystyle S' = S - 2\vert a_{pq}\vert^2$

(B.24)

The sequence of S's thus decrease monotonically. Since the sequence is bounded below by zero, and since we can choose $a_{pq}$ to be whatever element we want, the sequence can be made to converge to zero. Eventually one obtains a matrix

that is diagonal to machine precision. Thediagonal elements give the eigenvalues of the original matrix A, since

$\displaystyle D = R^{T} \cdot A \cdot R$

(B.25)

where

$\displaystyle R = P_1 \cdot P_2 \cdot P_3 \dots$

(B.26)

the

's being the successive Jacobi rotation matrices. The columns of

are the eigenvectors.

Emmanuel Branlard
http://emmanuel.branlard.free.fr/