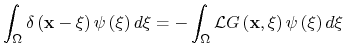Site perso : Emmanuel Branlard
C. The use of Green function for solving differential equations
Green's function
Where
If the differential equation is accompanied by appropriate boundary conditions, and if the green function corresponding to
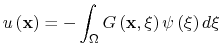 |
(C.3) |
The demonstration is straight forward. Multiplying equation C.1 by
![]() and integrating over the bounded space
and integrating over the bounded space ![]() with respect to
with respect to ![]() we have:
we have:
Due to the Dirac delta function property, the first term is simply:
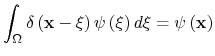 |
(C.5) |
Or, recalling the differential equation definition C.2:
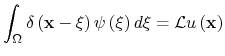 |
(C.6) |
Hence, equation C.4 may be rewritten as:
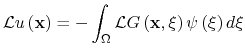 |
(C.7) |
Since
![]() is a linear differential operator, which does not act on the variable of integration we may write:
is a linear differential operator, which does not act on the variable of integration we may write:
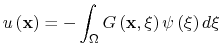 |
(C.8) |
Which is the integral representation presented above for ![]() . However, to evaluate this integral knowlagde of the explicit form of both
. However, to evaluate this integral knowlagde of the explicit form of both ![]() and
and ![]() are required. Furthermore, even if both
are required. Furthermore, even if both ![]() and
and ![]() are known, the associated integral may not be a trivial exercise. In addition, every linear differential operator does not admit a Green's Function. It would also be prudent to point out that in general, Green's functions are distributions rather than classical functions.
are known, the associated integral may not be a trivial exercise. In addition, every linear differential operator does not admit a Green's Function. It would also be prudent to point out that in general, Green's functions are distributions rather than classical functions.