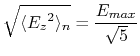Site perso : Emmanuel Branlard

• HOME
• Work
• Publications
• Contact
• Curriculum Vitae

• Papers
• Programs
• Music
• Linux
• Web sites

HOME workpapershtml2009fermi

7.5 Results summary

7.5.1 Fields calculation

For a uniform cylinder of radius $a$ and half length $b$ :

$$E_{z,int}(0,z_0) = - \frac{\rho}{2 \epsilon_0} \left[ -2z_0 + \frac{1}{2} \left( \fr... ...a^2+2\left(z_0-b\right)^2 }{ \sqrt{\left(z_0-b \right)^2+a^2} } \right) \right]$$ (7.33)

$$E_{z,ext}(0,z_0) = - \frac{\rho}{2 \epsilon_0} \left[ -2 b\: \text{sign}\left(z_0\ri... ...a^2+2\left(z_0-b\right)^2 }{ \sqrt{\left(z_0-b \right)^2+a^2} } \right) \right]$$ (7.34)

For a uniform spheroid of radius $a$ and half length $b$, the internal fields are :

$$\ a<b\ :$$ (7.35)

$$E_{z,int}(0,z_0) = - \frac{\rho}{\epsilon_0} \frac{1}{\frac{b^2}{a^2}-1} \left( 1-\frac{ \frac{b}{a}}{\sqrt{\frac{b^2}{a^2}-1}} \arg\cosh\frac{b}{a} \right) z_0$$ (7.36)

$$E_{z,ext}(0,z_0) = - \frac{\rho}{2\epsilon_0}a^2 b \left[\frac{\text{sign}(z_0)}{b^2... ...0\vert}{\sqrt{b^2-a^2}} \right)+\frac{\text{sign}(z_0)}{\sqrt{b^2-a^2}} \right]$$ (7.37) (7.38)

$$\ a>b\ :$$ (7.39)

$$E_{z,int}(0,z_0) = - \frac{\rho}{\epsilon_0} \frac{1}{\frac{b^2}{a^2}-1} \left( 1-\frac{ \frac{b}{a}}{\sqrt{1-\frac{b^2}{a^2}}} \arccos\frac{b}{a} \right) z_0$$ (7.40)

$$E_{z,ext}(0,z_0) = - \frac{\rho}{2\epsilon_0}a^2 b \left[-\frac{\text{sign}(z_0)}{a^... ...0\vert}{\sqrt{a^2-b^2}} \right)-\frac{\text{sign}(z_0)}{\sqrt{a^2-b^2}} \right]$$ (7.41)

For a uniform ellipsoid of semiaxes $r_x$, $r_y$, $r_z$, the internal fields are :

$$E_{x,int}(x) = \frac{1}{4\pi\epsilon_0} \frac{3I\lambda}{c\gamma^2}\frac{1-f}{r_x (r_x+r_y) r_z} x$$ (7.42)

$$E_{y,int}(y) = \frac{1}{4\pi\epsilon_0} \frac{3I\lambda}{c\gamma^2}\frac{1-f}{r_y (r_x+r_y) r_z} y$$ (7.43)

$$E_{z,int}(z) = \frac{1}{4\pi\epsilon_0} \frac{3I\lambda}{c}\frac{f}{r_x r_y r_z} z$$ (7.44)

7.5.2 RMS calculation

RMS calculations performed above are simple calculus and integrations. It is good to keep their values in mind, but to be convinced one often do the calculation at each time the value is needed. Let's write down the previous results in this section, so that we can refer to it later without doing the calculation again.

For a uniform cylinder( $x_0=y_0=r_0$):

$$x_ = \sqrt{\langle x^2 \rangle_n} = \frac{1}{2} x_0$$ (7.45)

$$r_ = \sqrt{\langle r^2 \rangle_n} = \frac{1}{\sqrt{2}} r_0\ (= \sqrt{2}\; x_ )$$ (7.46)

$$z_ = \sqrt{\langle z^2 \rangle_n} = \frac{1}{\sqrt{3}} z_0$$ (7.47)

$$z_ = \sqrt{\langle z^2 \rangle_n} = \frac{1}{\sqrt{12}} l_z$$ (7.48)

For a uniform spheroid( $x_0=y_0=r_0$):

$$x_ = \sqrt{\langle x^2 \rangle_n} = \frac{1}{\sqrt{5}} x_0$$ (7.49)

$$r_ = \sqrt{\langle r^2 \rangle_n} = \sqrt{\frac{2}{5}} r_0\ (=\sqrt{2}\; x_ )$$ (7.50)

$$z_ = \sqrt{\langle z^2 \rangle_n} = \frac{1}{\sqrt{5}} z_0$$ (7.51)

$$E_{z,\text{rms}} = \sqrt{\langle {E_z}^2 \rangle_n} = \frac{E_{max}}{\sqrt{5}}$$ (7.52)

Emmanuel Branlard
http://emmanuel.branlard.free.fr/