Site perso : Emmanuel Branlard
Subsections
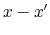 , while figure 10.2 displays the longitudinal phase space
, while figure 10.2 displays the longitudinal phase space 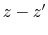 . Refer to table 10.1 for the distribution specification.
. Refer to table 10.1 for the distribution specification.
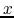 and
and  . If a simple linear relation exists, the behavior of the beam is different, and will not always expend if the correlation is negative. This might appear obvious, but when generating distributions for simulations, one can forget about this aspect of the beam. A beam is often modelised as a gaussian beam, and a correlation between
. If a simple linear relation exists, the behavior of the beam is different, and will not always expend if the correlation is negative. This might appear obvious, but when generating distributions for simulations, one can forget about this aspect of the beam. A beam is often modelised as a gaussian beam, and a correlation between 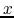 and
and  always exists. this justify the use of quadrupoles in beam line to focus or defocus the beam. Interpretation of these results in term of beam waist is done in the next section.
always exists. this justify the use of quadrupoles in beam line to focus or defocus the beam. Interpretation of these results in term of beam waist is done in the next section.
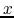 and
and 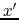 , the beam is focusing. Nevertheless the theory of gaussian beams predict that the transversal size of the beam will reach a minimum, the beam waist, before expending again. This effect is shown on figure
10.4. In the previous section, without any correlation, we were starting the simulation at the beam waist, and thus only observing an expension of the beam size. As the beam is focusing, the particle are more condensed and thus the space charge repulsion force become more important so that the beam waist is bigger if space charges are taken into account.
, the beam is focusing. Nevertheless the theory of gaussian beams predict that the transversal size of the beam will reach a minimum, the beam waist, before expending again. This effect is shown on figure
10.4. In the previous section, without any correlation, we were starting the simulation at the beam waist, and thus only observing an expension of the beam size. As the beam is focusing, the particle are more condensed and thus the space charge repulsion force become more important so that the beam waist is bigger if space charges are taken into account.
- 10.1.1 Simple case
- 10.1.2 Introducing transverse momentum correlation in the distribution
- 10.1.3 Beam waist interpretation
10.1 Theory without space charge
10.1.1 Simple case
We study here the evolution of the phase space for a drift of four meters. Figure 10.1 displays the transversal phase space

|

|
10.1.2 Introducing transverse momentum correlation in the distribution
The previous plots were done for a distribution where no correlation existed between
Figure 10.3 displays the plane ![]() for five different longitudinal positions. The distribution is the same than the previous one (table 10.1), exepts that initially, the correlation
for five different longitudinal positions. The distribution is the same than the previous one (table 10.1), exepts that initially, the correlation ![]() =-0.05
=-0.05 ![]() exists.
exists.

|
10.1.3 Beam waist interpretation
By introducing a negative correlation between
