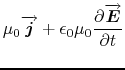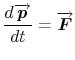HOME work papers html 2009fermi

1.1 Basic notions of Electromagnetism and charged particles

1.1.1 Electromagnetic fields: Maxwell equations

In a vacuum environment, electric charges and currents are related to electric fields $\v{E}$ and magnetic fields $\v{B}$ through the Maxwell equations:

$\displaystyle \v{\nabla} \times \v{E}$	=	$\displaystyle -\frac{\partial\v{B}}{\partial t}$		$\displaystyle \v{\nabla} \v{E}$	=	$\displaystyle \frac{\rho}{\epsilon_0}$
$\displaystyle \v{\nabla} \v{B}$	=	0		$\displaystyle \v{\nabla} \times \v{B}$	=	$\displaystyle \mu_0 \v{j} + \epsilon_0 \mu_0 \frac{\partial \v{E}}{\partial t}$

where $\rho$ is the density of the charges, $\v{v}$ the velocity, $\v{j}=\rho \v{v}$ the current, $\epsilon$ and $\mu$ the permittivity and permeability of the material(here the vacuum).

1.1.2 Lorentz Force

A particle of charge with velocity $\v{v}$ in an electromagnetic field, receives the external Lorentz force:

$\displaystyle \v{F} = q\left( \v{E} + \v{v}\times\v{B}\right)$

(1.1)

Charges can be expressed as multiples of the charge of an electron, . The charge of an electron being the elementary unit of electric charge: $e=-1.60217733\times 10^{-19}C$ . For high velocities and energies, a numerical application can reveal that for an equivalent force, it would be easier and less expensive if the force is generated by a magnetic field, rather than by an electric field. In general, the guidance and focusing of a beam in accelerator will thus be performed by magnetic elements. Nevertheless, at low energies, electric fields at radio frequencies will be prefered and thus relegated to the acceleration task.

1.1.3 Equation of motion

$\displaystyle \frac{d\v{p}}{dt}=\v{F}$

(1.2)

Where $\v{p}$ is the momentum. In the physics of accelerator , relativistic definition of the momemtum is used(see section 1.2).

Emmanuel Branlard
http://emmanuel.branlard.free.fr/