Subsections
1.2 Basic notions of relativity
The definition of the relativistic momentum is expressed in function of the rest mass
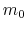
(for an electron
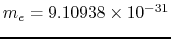 kg
kg):
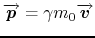 |
(1.3) |
The relativistic factor

being:
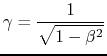 |
(1.4) |
The relative velocity
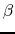
being:
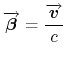 |
(1.5) |
The energy of a particle of rest mass
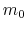
travelling at
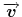
is:
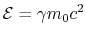 |
(1.6) |
The basic unit of energy used is the energy of a particule of charge

would gain while being accelerated between two conducting plates at a potential difference of one Volt: one electron volt (eV). By introducing the definitions of

,
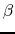
and
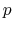
, we have the following expression for the energy:
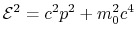 |
(1.7) |
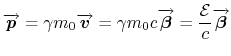 |
(1.8) |
The latter expression justify the expression of the momentum in the unit eV/c, instead of the classic mecanics one: kg m/s.
In the case of a conserved linear momentum, without external forces we can write:
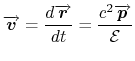 |
(1.9) |
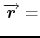 cst cst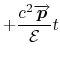 |
(1.10) |
In the four dimensional space, we consider two reference frames
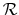
and
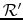
with a relative velocity
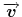
between them. The coordinates of a point in each frame are
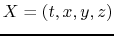
, and
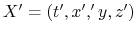
. The construction of Lorentz group transformation leads to the expression of any general Lorentz transformation:
where the coordinates from a frame to another are transformed by matricial multiplication by the Lorentz matrix

:
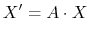 |
(1.13) |
The 4

4 matrix

, has null diagonal term. Its other terms can be expressed by six parameters(degree of freedom) and each of them can be decomposed on a base of 6 canonical 4

4 matrices

and

,

, the first ones being antisymmetric contrary to the second ones that are symmetric(refer to [
21] for the expression of these matrices).

and

are 3 dimensional vectors that can be respectively intepreted in term of rotation and boost of the coordinate axis of the frame
. The product

and

are thus tensorial products so that the result is a 4

4 matrix.
For a boost without rotation (

=0) in an arbitrary direction, the boost vector can be written in term of the relative velocity

:
 |
(1.14) |
The lorentz transformation matrix reduces then:
 |
(1.15) |
Choosing the prime notation to refer to parameters in the moving frame, the fields in the laboratory frame are obtained using the following Lorentz transformation[21]:
Using the hypothesis that  , the formulation reduces to:
, the formulation reduces to:
It can be noticed that in the common situation where

, the field in the laboratory frame will be reduced to:
 |
(1.20) |
Thus, the two fields are the same for any velocity in the hypothesis of pure longitudinal momentum.
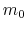 (for an electron
(for an electron
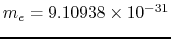 kg):
kg):
 being:
being:
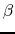 being:
being:
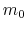 travelling at
travelling at 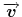 is:
is:
 would gain while being accelerated between two conducting plates at a potential difference of one Volt: one electron volt (eV). By introducing the definitions of
would gain while being accelerated between two conducting plates at a potential difference of one Volt: one electron volt (eV). By introducing the definitions of  ,
, 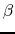 and
and 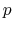 , we have the following expression for the energy:
, we have the following expression for the energy:
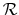 and
and
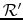 with a relative velocity
with a relative velocity 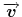 between them. The coordinates of a point in each frame are
between them. The coordinates of a point in each frame are
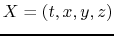 , and
, and
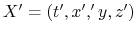 . The construction of Lorentz group transformation leads to the expression of any general Lorentz transformation:
. The construction of Lorentz group transformation leads to the expression of any general Lorentz transformation:
 :
:
 4 matrix
4 matrix  , has null diagonal term. Its other terms can be expressed by six parameters(degree of freedom) and each of them can be decomposed on a base of 6 canonical 4
, has null diagonal term. Its other terms can be expressed by six parameters(degree of freedom) and each of them can be decomposed on a base of 6 canonical 4 4 matrices
4 matrices  and
and  ,
,
 , the first ones being antisymmetric contrary to the second ones that are symmetric(refer to [21] for the expression of these matrices).
, the first ones being antisymmetric contrary to the second ones that are symmetric(refer to [21] for the expression of these matrices).
 and
and
 are 3 dimensional vectors that can be respectively intepreted in term of rotation and boost of the coordinate axis of the frame
are 3 dimensional vectors that can be respectively intepreted in term of rotation and boost of the coordinate axis of the frame
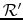 . The product
. The product
 and
and
 are thus tensorial products so that the result is a 4
are thus tensorial products so that the result is a 4 4 matrix.
4 matrix.
 =0) in an arbitrary direction, the boost vector can be written in term of the relative velocity
=0) in an arbitrary direction, the boost vector can be written in term of the relative velocity  :
:
 , the field in the laboratory frame will be reduced to:
, the field in the laboratory frame will be reduced to:
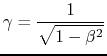
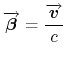
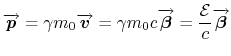
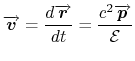
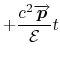



![]() , the formulation reduces to:
, the formulation reduces to:


