Site perso : Emmanuel Branlard
Subsections
 , the potential on any point
, the potential on any point  of this axis can be expressed using the Biot and Savart law:
of this axis can be expressed using the Biot and Savart law:
Where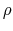 is the density of charges. For a cylinder of semi-axis
is the density of charges. For a cylinder of semi-axis  and radius
and radius  with
with  charges we have:
charges we have:
We first integrate equattion 6.1 along , between
, between  and
and  , and then do the change of variable
, and then do the change of variable  :
:
Eventually, for a cylindrical distribution, the potentiall inside ( , subscribt ``int''), and outside(
, subscribt ``int''), and outside( , subscribt ``ext'') the distribution are:
, subscribt ``ext'') the distribution are:
 on the axis can be expressed:
on the axis can be expressed:
 , the RMS value of the longitudinal bunch half-length, and
, the RMS value of the longitudinal bunch half-length, and  , the rms value of the radius. Table 6.1 display the parameters used for the simulation.
, the rms value of the radius. Table 6.1 display the parameters used for the simulation.
- 6.1.1 Theoretical expression of the potential
- 6.1.2 Theoretical expression of the Fields for the cylinder
- 6.1.3 Graphical comparisons
6.1 Fields for a cylindrical distribution
6.1.1 Theoretical expression of the potential
Given a homogeneous distribution of charges in a cylindrical volume with revolution symetry around the longitudinal axisWhere
 |
(6.2) |
We first integrate equattion 6.1 along
The integration of the second term is:
![]()
The first part is calculated eather by blindly applying a formula we provide in annex F or by simply writting
![]() , leading to so a sum of two integrals, where the integration by part of the second one leads to the original integral:
, leading to so a sum of two integrals, where the integration by part of the second one leads to the original integral:
![$\displaystyle \int \sqrt{1+z^2} = \Big[ \arg\sinh z \Big] + \Big[z \sqrt{1+z^2} \Big] -\int \sqrt{1+z^2}$](img362.gif) |
(6.4) |
Eventually, for a cylindrical distribution, the potentiall inside (
The function argsinh is the inverse functions of sinh, the hyperbolic sine.
6.1.2 Theoretical expression of the Fields for the cylinder
From the previous expression of the potential, the field component|
|
6.1.3 Graphical comparisons
On figure 6.1 one can see the good agreement between the numerical (solid colored line) and the theoretical(dashed lines) fields for different values of

|
 d
d d
d
![$\displaystyle \left. \left. \left(z_0+b \right)\sqrt{\left(z_0+b \right)^2+a^2} -\left(z_0-b \right)\sqrt{\left(z_0-b \right)^2+a^2} \ \right] \ \right\}$](img368.gif)

![$\displaystyle - \frac{\rho}{2 \epsilon_0} \left[
-2z_0 + \frac{1}{2} \left( \fr...
...a^2+2\left(z_0-b\right)^2 }{ \sqrt{\left(z_0-b \right)^2+a^2} } \right) \right]$](img373.gif)
![$\displaystyle - \frac{\rho}{2 \epsilon_0} \left[ -2 b\: \text{sign}\left(z_0\ri...
...a^2+2\left(z_0-b\right)^2 }{ \sqrt{\left(z_0-b \right)^2+a^2} } \right) \right]$](img375.gif)