Subsections
We will call spheroid an ellipsoid with radial symmetry.
Like in the previous section, the Biot and Savart law can be integrated to obtain a theoretical expression of the potentials and fields for an ellipsoidal distribution. Given a homogeneous distribution of charges in an ellipsoidal volume with revolution symetry around the longitudinal axis

, the potential on any point

of this axis can be expressed using the Biot and Savart law:
Where
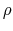
is the density of charges. For an ellipse of semi-axes lengths

we have:
 |
(6.10) |
The integration on all charges is reduced to the domain defined by the plane ellipse driven by the equation:
 |
(6.11) |
This defines the boundaries used for the integration. We first integrate along

, between

and

:
 d d |
(6.12) |
The integration along

requires the distinction between the case

and

. Moreover, one has to distinguish the case

, for the potential inside the bunch, and

for the external potential. The integration is a little bit more complicated than the one for the cylindrical case. One can refer to Annex
F for some mathematical refreshments. After the integration, the fields are generalized[
28] to points off axis but inside the distribution. For

and

the potential in the spheroid is:
![$\displaystyle \Phi(x_0,y_0,z_0)_{int} = \Phi_0- \frac{\rho}{2 \epsilon_0} \left...
...ac{ \frac{b}{a}}{\sqrt{\frac{b^2}{a^2}-1}} \arg\cosh\frac{b}{a} \right) \right]$](img391.gif) |
(6.13) |
While the external potential( ) on the axis would be:
) on the axis would be:
![$\displaystyle \Phi(0,z_0)_{ext} = \frac{\rho}{2 \epsilon_0} a^2 b \left[ \frac{...
...frac{1}{\sqrt{b^2-a^2}} \arg\coth \frac{\vert z_0\vert}{\sqrt{b^2-a^2}} \right]$](img392.gif) |
(6.14) |
Now, for an ellipsoid of dimensions such that  , the potential is :
, the potential is :
![$\displaystyle \Phi(x_0,y_0,z_0)_{int} = \Phi_0- \frac{\rho}{2 \epsilon_0} \left...
...frac{ \frac{b}{a}}{\sqrt{1-\frac{b^2}{a^2}}} \arccos\frac{b}{a} \right) \right]$](img393.gif) |
(6.15) |
![$\displaystyle \Phi(0,z_0)_{ext} = \frac{\rho}{2 \epsilon_0} a^2 b \left[ -\frac...
...{1}{\sqrt{a^2-b^2}} \text{arccotg}\frac{\vert z_0\vert}{\sqrt{a^2-b^2}} \right]$](img394.gif) |
(6.16) |
The functions argcosh and argcoth are the respective inverse functions of cosh and coth, the hyperbolic cosine and cotangent. The generalization of the external fields is more complicated and we refr the reader to [28].
From the previous expression of the internal potential, it can be immediatly seen that a linear dependence is expected between each field component and its corresponding axes.
 |
(6.17) |
With the symmetry of the distribution imposing

. Deriving equation
6.15 for the case

yields to:
While for the case

:
In [
30],refering [
22], the following expressions can be found for

:
 |
(6.21) |
with the excentricity

. Nevertheless, no link between
6.22 and
6.23 has not been done yet.
The expression of the external field being more complicated we will focus on its expression on the ellipse axis ( ) and its longitudinal component.
For the case
) and its longitudinal component.
For the case  :
:
![$\displaystyle E_{z,ext}(0,z_0)= - \frac{\rho}{2\epsilon_0}a^2 b \left[\frac{\te...
...\vert}{\sqrt{b^2-a^2}} \right)+\frac{\text{sign}(z_0)}{\sqrt{b^2-a^2}} \right ]$](img405.gif) |
(6.22) |
And for  :
:
![$\displaystyle E_{z,ext}(0,z_0)= - \frac{\rho}{2\epsilon_0}a^2 b \left[-\frac{\t...
...\vert}{\sqrt{a^2-b^2}} \right)-\frac{\text{sign}(z_0)}{\sqrt{a^2-b^2}} \right ]$](img406.gif) |
(6.23) |
The linearity of the fields with respect to their axis is still valid in the general case of an ellipsoid. Approximate expressions have been derived by Lapostolle[
28] and are used by the software trace 3D[
8] to compute the space charge fields. For an ellipsoid of semiaxes

,

,

, the following expressions are given:
where

is a function of

,

the free space wave-length of the RF and

the average current assuming one bunch is emitted at each period of the RF. As the result of this, in the case of a single bunch,

and eventually equation
6.28 can be written:
 |
(6.27) |
The fact that

is called the form factor appears then obvious.
Figure 6.2(a) gives reference values for the form factor and figure 6.2(b) represent these values spline-interpolated for more precision.
Figure 6.2:
Form factor data and corersponding plot for different value of p
|
|
[]
| p |
f |
1/p |
f |
| 0.0000 |
1.0000 |
0.0000 |
0.0000 |
| 0.0500 |
0.9260 |
0.0500 |
0.0070 |
| 0.1000 |
0.8610 |
0.1000 |
0.0200 |
| 0.1500 |
0.8030 |
0.1500 |
0.0370 |
| 0.2000 |
0.7500 |
0.2000 |
0.0560 |
| 0.2500 |
0.7040 |
0.2500 |
0.0750 |
| 0.3000 |
0.6610 |
0.3000 |
0.0950 |
| 0.3500 |
0.6230 |
0.3500 |
0.1150 |
| 0.4000 |
0.5880 |
0.4000 |
0.1350 |
| 0.4500 |
0.5560 |
0.4500 |
0.1550 |
| 0.5000 |
0.5270 |
0.5000 |
0.1740 |
| 0.5500 |
0.5000 |
0.5500 |
0.1920 |
| 0.6000 |
0.4760 |
0.6000 |
0.2100 |
| 0.6500 |
0.4530 |
0.6500 |
0.2270 |
| 0.7000 |
0.4320 |
0.7000 |
0.2440 |
| 0.7500 |
0.4130 |
0.7500 |
0.2600 |
| 0.8000 |
0.3940 |
0.8000 |
0.2760 |
| 0.8500 |
0.3780 |
0.8500 |
0.2910 |
| 0.9000 |
0.3620 |
0.9000 |
0.3060 |
| 0.9500 |
0.3470 |
0.9500 |
0.3200 |
| 1.0000 |
0.3330 |
1.0000 |
0.3330 |
|
|
[]

|
|
On figure
6.3 one can see the good agreement between the numerical (solid colored line) and the theoretical(dashed lines) fields for different values of

, the RMS value of the bunch length, and

, the rms value of the radius. Table
6.2 display the parameters used for the simulation.
Figure 6.3:
Ellipsoidal distribution: Longitudinal field  along z - comparison between simulation and theory. The theoretical fields are represented with black dashed lines. A perfect agreement is found, but the maximum amplitude of the simulated field is always smaller. This depends on the resolution of the grid, and the smoothing of the fields.
along z - comparison between simulation and theory. The theoretical fields are represented with black dashed lines. A perfect agreement is found, but the maximum amplitude of the simulated field is always smaller. This depends on the resolution of the grid, and the smoothing of the fields.
|
|
Figure 6.4:
Comparison of theoretical (dashed) and numerical longitudinal field. for an ellipsoidal bunch at two different energies: a) 0 Mev, b)100 MeV - Values calculated on the grid are displayed with green cross. Note that a small amount of cells has been used here.
 (a)
 (b)
|
 , the potential on any point
, the potential on any point  of this axis can be expressed using the Biot and Savart law:
of this axis can be expressed using the Biot and Savart law:
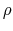 is the density of charges. For an ellipse of semi-axes lengths
is the density of charges. For an ellipse of semi-axes lengths  we have:
we have:
 , between
, between  and
and
 :
:
 requires the distinction between the case
requires the distinction between the case  and
and  . Moreover, one has to distinguish the case
. Moreover, one has to distinguish the case  , for the potential inside the bunch, and
, for the potential inside the bunch, and  for the external potential. The integration is a little bit more complicated than the one for the cylindrical case. One can refer to Annex F for some mathematical refreshments. After the integration, the fields are generalized[28] to points off axis but inside the distribution. For
for the external potential. The integration is a little bit more complicated than the one for the cylindrical case. One can refer to Annex F for some mathematical refreshments. After the integration, the fields are generalized[28] to points off axis but inside the distribution. For  and
and  the potential in the spheroid is:
the potential in the spheroid is:
 . Deriving equation 6.15 for the case
. Deriving equation 6.15 for the case  yields to:
yields to:
 :
:
 :
:
 . Nevertheless, no link between 6.22 and 6.23 has not been done yet.
. Nevertheless, no link between 6.22 and 6.23 has not been done yet.
 ,
,  ,
,  , the following expressions are given:
, the following expressions are given:
 is a function of
is a function of
 ,
,  the free space wave-length of the RF and
the free space wave-length of the RF and  the average current assuming one bunch is emitted at each period of the RF. As the result of this, in the case of a single bunch,
the average current assuming one bunch is emitted at each period of the RF. As the result of this, in the case of a single bunch,
 and eventually equation 6.28 can be written:
and eventually equation 6.28 can be written:
 is called the form factor appears then obvious.
is called the form factor appears then obvious.
 , the RMS value of the bunch length, and
, the RMS value of the bunch length, and  , the rms value of the radius. Table 6.2 display the parameters used for the simulation.
, the rms value of the radius. Table 6.2 display the parameters used for the simulation.
 d
d

 d
d![]() ) on the axis would be:
) on the axis would be:
![$\displaystyle \Phi(0,z_0)_{ext} = \frac{\rho}{2 \epsilon_0} a^2 b \left[ \frac{...
...frac{1}{\sqrt{b^2-a^2}} \arg\coth \frac{\vert z_0\vert}{\sqrt{b^2-a^2}} \right]$](img392.gif)
![]() , the potential is :
, the potential is :
![$\displaystyle \Phi(x_0,y_0,z_0)_{int} = \Phi_0- \frac{\rho}{2 \epsilon_0} \left...
...frac{ \frac{b}{a}}{\sqrt{1-\frac{b^2}{a^2}}} \arccos\frac{b}{a} \right) \right]$](img393.gif)
![$\displaystyle \Phi(0,z_0)_{ext} = \frac{\rho}{2 \epsilon_0} a^2 b \left[ -\frac...
...{1}{\sqrt{a^2-b^2}} \text{arccotg}\frac{\vert z_0\vert}{\sqrt{a^2-b^2}} \right]$](img394.gif)
![]() ) and its longitudinal component.
For the case
) and its longitudinal component.
For the case ![]() :
:
![$\displaystyle E_{z,ext}(0,z_0)= - \frac{\rho}{2\epsilon_0}a^2 b \left[\frac{\te...
...\vert}{\sqrt{b^2-a^2}} \right)+\frac{\text{sign}(z_0)}{\sqrt{b^2-a^2}} \right ]$](img405.gif)
![]() :
:
![$\displaystyle E_{z,ext}(0,z_0)= - \frac{\rho}{2\epsilon_0}a^2 b \left[-\frac{\t...
...\vert}{\sqrt{a^2-b^2}} \right)-\frac{\text{sign}(z_0)}{\sqrt{a^2-b^2}} \right ]$](img406.gif)

 (a)
(a)
 (b)
(b)
![$\displaystyle \Phi(x_0,y_0,z_0)_{int} = \Phi_0- \frac{\rho}{2 \epsilon_0} \left...
...ac{ \frac{b}{a}}{\sqrt{\frac{b^2}{a^2}-1}} \arg\cosh\frac{b}{a} \right) \right]$](img391.gif)







