Subsections
7.2 Spheroidal distribution
We have seen in the previous section that the fields inside the ellipsoid are linear with respect to their axis. We will write equation
6.28 as:
 |
(7.5) |
without expliciting the constants hidden behind the positive constant

. The maximum of the longitudinal field in the distribution is:
 |
(7.6) |
Then we can write the field in function of its maximum:
 |
(7.7) |
By definition
 |
(7.8) |
Projecting the density distribution function of the ellipsoid on the z-axis:
 |
(7.9) |
where the projection of the density function of the distribution of a uniform ellipsoid is:
![$\displaystyle f(z)=\int_{x,y} f(x,y,z) dxdy = \left[ 1 -\left(\frac{z}{Z_0}\right)^2\right] A$](img430.gif) |
(7.10) |
The constant
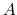
arbitrary chosen at 1. Let's present some intermediate steps of calculus:
The rms value of  is then
is then
 |
(7.14) |
And
 |
(7.15) |
: We will study the RMS value of

for different radius. We will then use RMS value of the radius.
As it is a spheroid we could simply write

and thus:
 |
(7.16) |
But let's be convinced that we are right. Tha calculation is done for the section

. We write

, and calculate the not-normalized rms value of x:
 |
(7.17) |
The nomalisation being:
 |
(7.18) |
we end up with
 |
(7.19) |
On the other end we have
 |
(7.20) |
So eventually we have:
 |
(7.21) |
By symmetry, from the calculation of

we have:
 |
(7.22) |
and thus, as

:
 |
(7.23) |
: Two different methods were used for the RMS calculation of the simulated field.
The first one, is labelled
(sim.) in the legend of figure
7.1, and the second one
(sim. from max).
Going back to the definition of the rms value, the first method consists in calculating the rms value from the field value on each particle. For this, we added a little ``FOR'' loop at the end of the main of our stand alone algorithm:
astraimpulse_main.f. For each component of the two fields, the rms value is calculated as follow:
 |
(7.24) |
where
 part
part is the number of particle,

,

,

, its coordinates and

has been calculated with the function
SCGridInterpolate. The 6 RMS values are stored in an output file called
RMSFields.out
The second method used is based on the theoretical rms value calculated above. Knowing the maximum of the simulated longitudinal field on the z-axis, divinding it by  provides a results comparable to the theoretical RMS value. To know the longitudinal field on the z-axis, we will use the file E_DIR.out, which is outputed by our main program. This functionnality will be developped in details in section 8.1.3.
provides a results comparable to the theoretical RMS value. To know the longitudinal field on the z-axis, we will use the file E_DIR.out, which is outputed by our main program. This functionnality will be developped in details in section 8.1.3.
Figure 7.1:
Rms value of the longitudinal field for a spheroidal distribution. The theoretical value is calculated with the formula developped in the previous section, taking
 rms
rms max
max . Calculating the simulated rms value(sim.) by averaging the longitudinal field on each particle, provides a really good agreement with the theory. From the maximum of the simulated field, another RMS value can be defined by dividing it by
. Calculating the simulated rms value(sim.) by averaging the longitudinal field on each particle, provides a really good agreement with the theory. From the maximum of the simulated field, another RMS value can be defined by dividing it by  . Nevertheless, we previously saw that the simulated field has a smaller maximum. This explains why the values sim. from max are smaller. Data points are stored in file /results/ez-rms/MErmsEllipse.csv
. Nevertheless, we previously saw that the simulated field has a smaller maximum. This explains why the values sim. from max are smaller. Data points are stored in file /results/ez-rms/MErmsEllipse.csv
|
|
Figure 7.2:
Maximum value of the longitudinal field for a spheroidal distribution. Once again we see that the simulated field has an amplitude smaller than the theoretical one. Note that the fields are here plotted with the real length of the bunch and the real radius of the bunch, instead of RMS values.
|
|
 . The maximum of the longitudinal field in the distribution is:
. The maximum of the longitudinal field in the distribution is:
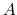 arbitrary chosen at 1. Let's present some intermediate steps of calculus:
arbitrary chosen at 1. Let's present some intermediate steps of calculus:
 for different radius. We will then use RMS value of the radius.
As it is a spheroid we could simply write
for different radius. We will then use RMS value of the radius.
As it is a spheroid we could simply write
 and thus:
and thus:
 . We write
. We write
 , and calculate the not-normalized rms value of x:
, and calculate the not-normalized rms value of x:
 we have:
we have:
 :
:
 part is the number of particle,
part is the number of particle,  ,
, ,
, , its coordinates and
, its coordinates and  has been calculated with the function SCGridInterpolate. The 6 RMS values are stored in an output file called RMSFields.out
has been calculated with the function SCGridInterpolate. The 6 RMS values are stored in an output file called RMSFields.out



![$\displaystyle f(z)=\int_{x,y} f(x,y,z) dxdy = \left[ 1 -\left(\frac{z}{Z_0}\right)^2\right] A$](img430.gif)



![]() is then
is then







![]() provides a results comparable to the theoretical RMS value. To know the longitudinal field on the z-axis, we will use the file E_DIR.out, which is outputed by our main program. This functionnality will be developped in details in section 8.1.3.
provides a results comparable to the theoretical RMS value. To know the longitudinal field on the z-axis, we will use the file E_DIR.out, which is outputed by our main program. This functionnality will be developped in details in section 8.1.3.


