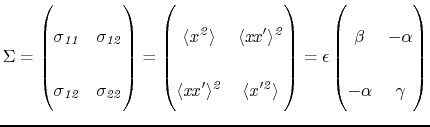HOME work papers html 2009fermi

9.4 Note on the sigma matrix outputed by Astra

The reader is invited to read chapter 3.2 for a better understanding on beam matrix and emittance. For convenience, we recall here some formulas:

$\displaystyle \epsilon_x=\sqrt{\langle x^2\rangle \langle x'^2\rangle-\langle xx'\rangle^2}$

(9.4)

$\displaystyle \epsilon_{nx}=\frac{1}{m_0 c}\sqrt{\langle x^2\rangle \langle p_x^2\rangle-\langle xp_x\rangle^2}$

(9.5)

$\displaystyle \epsilon_{nx}= \beta \gamma \epsilon_x$

(9.6)

$\displaystyle \Sigma = \begin{pmatrix}{\it\sigma_{11}} & {\it\sigma_{12}}\\ {\i... ...rix} = \epsilon \begin{pmatrix}\beta &-\alpha\\ -\alpha& \gamma\\ \end{pmatrix}$

(9.7)

$\displaystyle \epsilon = \frac{A}{\pi} = a b$

(9.8)

9.4.1 Analysing the previous algorithm without the source code

Philippe Piot added to Astra the functionnality of outputing the $\Sigma$ matrix if the option SigmaS is specified in the &NEWRUN section of the run file. The structure of the output file is specified in table 9.1. The matrix being symmetric only 21( $6\times6/2+6/2$ ) coefficients need to be stored. The two first columns contain the position and the energy. The following 21 are the matrix coefficients.

Table 9.1: Structure of the file containing the sigma matrix: run.Sigma.001

1	2	3	4	...	8	9	10	...	22	23
z	$\mathcal{E}$	$\sigma_{11}$	$\sigma_{12}$	...	$\sigma_{16}$	$\sigma_{22}$	$\sigma_{23}$	...	$\sigma_{56}$	$\sigma_{66}$

A sigma matrix can be written in different units, and attention has been paid to plot the ellipse with the right dimension and units on each axis. To check this, we calculated directly the sigma matrix from the distribution, and we compared it with the matrix outputed by Astra. We did this for two cylinders with with two different normalized transversal emittances : $\epsilon _{nx}=5$ mrad.mm and $\epsilon_{nx}=1$ mrad.mm. See table 9.2 for more information on the distributions.

Parameter	Value
Type	Uniform cylinder
$\sigma_x$	1 mm
$\sigma_y$	1 mm
$\sigma _z$	0.4 mm
$\epsilon_{nx}$ , `NEmit_x`	{1 ; 5 } mrad.mm
Energy $\mathcal{E}$	15 MeV
Charge	-0.25 nC
part	10000

The 2D x-block of the matrix outputed by astra were:

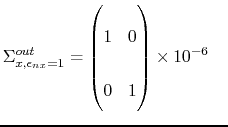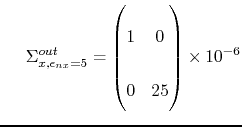$\displaystyle \Sigma_{x,\epsilon_{nx}=1}^{out}=\begin{pmatrix}1&0\\ 0&1\\ \end{pmatrix}\times 10^{-6} \ \ \$ and $\displaystyle \ \ \ \ \Sigma_{x,\epsilon_{nx}=5}^{out}= \begin{pmatrix}1&0\\ 0&25\\ \end{pmatrix}\times 10^{-6}$

(9.9)

One can easily notice that the square root of the determinant of these matrix provides the normalized emittance in [m.rad]. From the input distribution, the values $\sigma_{x}$ , $\sigma_{p_x}$ , $\sigma_{\tilde{p}_x}$ and $\sigma_{x'}$ have been calculated, remembering our notation for the momentum variable in Astra: $\tilde{p}_x=p_x/m_0c=\gamma\beta_x$ . The units for these four values are respectively: [m], [eV/c], [.] and [rad]. From the comparison we concluded that the matrix outputed by astra was the following:

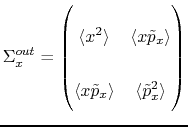$\displaystyle \Sigma_{x}^{out}= \begin{pmatrix}\langle x^2 \rangle & \langle x\... ... \langle x\tilde{p}_x \rangle & \langle {\tilde{p}_x}^2\rangle \\ \end{pmatrix}$

(9.10)

Nevertheless, the canonical variables in phase space are

instead of $x-\tilde{p}_x$ , and the most commun set used is

. In the first case, one simply goes from dimensionless units [.] to [MeV/c] by using:

$\displaystyle p_x\:$ [MeV/c] $\displaystyle = \left(\tilde{p}_x\:[.]\right) \times \left(m_0 c\: \text{[MeV/c]}\right)$

(9.11)

where the product $m_0 c = 0.510998 \simeq 0.511$ [MeV/c]. And thus, the sigma matrix in the space

can be calculated, and has the following terms:

$\displaystyle \sigma_{12}$	$\displaystyle =$	$\displaystyle \langle x p_x \rangle \simeq 0.511 \langle x \tilde{p}_x \rangle$	(9.12)
$\displaystyle \sigma_{22}$	$\displaystyle =$	$\displaystyle \langle p_x^2 \rangle \simeq 0.511^2 \langle \tilde{p}_x^2 \rangle$	(9.13)

The correponding ellipse is plotted with horizontal and vertical units being respectively [m] and [MeV/c]. For the phase space

we use the relation:

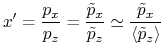$\displaystyle x'=\frac{p_x}{p_z}=\frac{\tilde{p}_x}{\tilde{p}_z} \simeq \frac{\tilde{p}_x}{ \langle \tilde{p}_z \rangle }$

(9.14)

where $\langle \tilde{p}_z \rangle$ stands for the mean value of $\tilde{p}_z$ . Nevertheless, this value, close to $\gamma\beta$ , is unknown in general with the single knowledge of the $\Sigma$ matrix. We will then use another output file of Astra, the file: run.ref.001, which contains the value of

, and $\bar{p_z} [MeV/c]$ . One has to be carefull because the number of lines of run.ref.001 and run.Sigma.001 are in general different, so the

column must be used to find the indices for which the

values of the two files are the closest. We will then write

$\displaystyle \langle \tilde{p}_z \rangle \; [.] = \frac{ \langle p_z \rangle \; \text{[MeV/c]} }{0.511\; \text{[MeV/c]}}$

(9.15)

So that eventually, the $\Sigma$ matrix, in the phase space

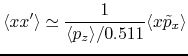$\displaystyle \sigma_{12}$	$\displaystyle =$	$\displaystyle \langle x x'\rangle \simeq \frac{1}{ \langle p_z \rangle / 0.511} \langle x \tilde{p}_x \rangle$	(9.16)
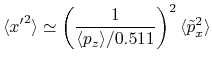$\displaystyle \sigma_{22}$	$\displaystyle =$	$\displaystyle \langle {x'}^2 \rangle \simeq \left( \frac{1}{\langle p_z \rangle / 0.511}\right)^2 \langle \tilde{p}_x^2 \rangle$	(9.17)

The corresponding ellipse is plotted with horizontal and vertical units being respectively [m] and [rad].

To illustrate the difference between the ellipse representation and the real distribution in the phase space we chose first to use a uniform distribution of particules in the transversal direction. In this case, if $\sigma_x=1$ [mm], the radius of the bunch will be $2 \sigma_x$ . This is observed on figure 9.1 for the three sets of parameters , , and $x-\tilde{p_x}$ . One can verify that the RMS values (i.e. the ellipse semi-axes) $x_{rms}$ , $x'_{rms}$ correspond exactly to the values contained in the files run.Xemit.001 and run.Yemit.001, confirming that the algorithm plotting the ellipses from the covariance matrix it consistent.

**Figure 9.1:** Phase space ellipse for a cylinder of emittance $\epsilon _{nx}=5$ mmrad.mm. for different set of parameters and units. (a) - (b) - (c) $x-\tilde{p_x}$ . See table 9.2 for details on the cylindrical distribution used. The distribution along is uniform, as well as the distribution of the momentum , thus explaining this rectangular shape when plotted in the phase space. The ellipse plotted in the middle is the translation of the sigma matrix in terms of twiss-parameters, with the adapted units for each case. Figure (c) is in the canonical dimensions $x-\tilde{p_x}$ , so that, when multiplying the axis lengths of the ellipse, one gets the normalised emittance : 5 mrad.mm
(a) (b) (c)

**Figure 9.2:** Phase space ellipse for an ellipsoidal distribution with gaussian momentum. : (a) gaussian ellipsoid - (b) uniform ellipsoid.
(a) (b)

9.4.2 Modifying the source code to output a standard sigma matrix

The main part of this work was not the implementation itself, but the understanding of the units and dimensions as well as what should be plotted as an ellipse in the phase space. The previous section, might be a little hard to read, but it really translates the methodical approach used to be sure that we output and plot the right sigma matrix / ellipse. After modification of the fortran source file X_em_mon.f, Astra is now outputing a file run.Sigmas.001 which has the following structure (table 9.3).

Column 1 2 3 4 ... 8 9 10 ... 22 23

Variable z PZ_meanU $\sigma_{11}$ $\sigma_{12}$ ... $\sigma_{16}$ $\sigma_{22}$ $\sigma_{23}$ ... $\sigma_{56}$ $\sigma_{66}$

Value z $\gamma \beta_z$ $\langle x^2\rangle$ $\langle xx'\rangle$ ... $\langle xz'\rangle$ $\langle {x'}^2\rangle$ $\langle x' y\rangle$ ... $\langle z z' \rangle$ $\langle {z'}^2 \rangle$

Units [m] [ . ] [m] [m rad] ... [m .] [rad] [m rad] ... [m .] [ . ]

Emmanuel Branlard
http://emmanuel.branlard.free.fr/