Subsections
In its most general form, the solution of the wave equation is expressed with Bessel functions. For a
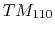
cavity, it can be shown that the longitudinal field is of the following form:
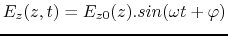 |
(14.1) |
where
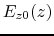
is in a good approximation equal to
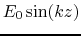
, with

fixing the field oscillation frequency with time,

being the space pulsation, and

being a phase constant that can be fixed. The phase value is very important because the phase space evolution through the cavity will mainly depend on the chosen phase.
14.1.2 Correlation introduced by a cavity between  and the energy
and the energy
Lets introduce a bunch into the cavity and determine its gain in energy. The field seen by a particle P when it is at a position

and a time

inside the cavity is written
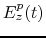
. Of course the trajectory of the particle provides a relation
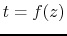
such that the field seen by a particle in the cavity is only a function of

. In an accelerating cavity this relation would be complex, but as the particles are travelling at a relativistic speed, we will assume that the reference particle has the following trajectory
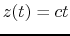
, and the other particles to have the trajectory
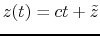
.
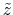
being the distance with respect to the reference particle, and the dispersion becoming
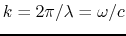
. Given these definitions, the field seen by a particle of the bunch at the position

in the cavity is:
 |
(14.2) |
The hypothesis of relativistic speed imply that 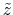 is a constant for a given particle. We will thus introduced the phase
is a constant for a given particle. We will thus introduced the phase
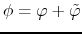 with
with
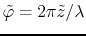 . This traduce that the difference of arrival time in the cavity between the particles of the bunch can be expressed by a difference of phase in the expression of the field.
The total energy gained by a particle during its travel through the caviy is then obtained by calculating the following integreal:
. This traduce that the difference of arrival time in the cavity between the particles of the bunch can be expressed by a difference of phase in the expression of the field.
The total energy gained by a particle during its travel through the caviy is then obtained by calculating the following integreal:
![$\displaystyle \int_{z=0}^{z=l_c} \left[ \cos(\phi)-\cos({2kz+\phi}) \right]dz = \frac{1}{2k}\left[ \sin(\phi+2kl_c)-sin(\phi) \right] +l_c \cos(\phi)$](img644.gif) |
(14.3) |
But as the design of a cavity is such that the length of the cavity
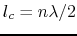
(
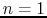
corresponding to the
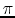
mode) for the bunch to see a field of a constant sign, the term between the brakets reduces to 0. Replacing

by its expression leads us eventually with:
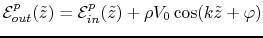 |
(14.4) |
Thus, for the reference particle:
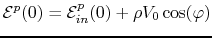 |
(14.5) |
The difference of the two last expression, gives us the evolution of the energy space phase coordinates through the cavity:
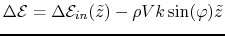 |
(14.6) |
Or, by writting this expression in term of momentum:
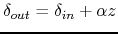 |
(14.7) |
Expression in which we can see that a linear dependence has been introduced by the cavity between the momentum and the longitudinal coordinate. The slope of this correlation,

, is directly proportional to
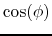
, where we remind that

is the phase parameter of the cavity. This parameter can easily be adapted to satisfy a requirement on

or

.
Figure 14.1:
Fermilab cavity schema and picture. a)shcema b)picture
 (a)
 (b)
|
The fields we have is a picture of the time depending fields. To make them be time dependent astra will multiply them by a time depending sine function.
The same is done for the other components of E and B.
As we included in our field map the two small pipes surrounding the cavity, the best way to adjust the phase is to adjust it in reference to the middle of the cavity. Indeed, at
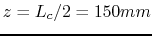
, we are in the middle of the third cell. In order to have the right kick at the right position we chose

such that the sine is equal to minus one at
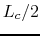
, ie:
 |
(14.8) |
We find

= 287.58 degrees. Figure
14.2 represents the
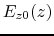
and the sine function of z. The product of the two give us the field seen by the particle with z, and we can see that it will be positive all along the trajectory.
Figure 14.2:
 (red) in MV/m and the sine oscillating function (blue) adjusted in phase without scale
(red) in MV/m and the sine oscillating function (blue) adjusted in phase without scale
|
|
As the fields were generated by , arbitrary values of the power given to the cavity were inputed. As a result of this, the fields have to be scaled to their real values by multiplying all the E and B components by a same scaling factor.
Astra has his own scale factor algorythm, but it uses the maximum E value on the cavity axis. With the
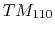
mode we use, the electric field is equal to zero on the axis, so this method is unefficient.
We used a method consisting in integrating
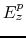
along the axis
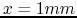
,

, and compare the voltage value with the real one: 45kV.
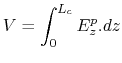 |
(14.9) |
Numerically we have data every
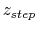
, and assuming that the function under the integral is constant between two steps then, it leads us to:
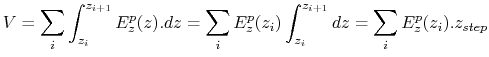 |
(14.10) |
We find
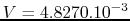 V/m, and a scale of 9.3227e+6 to have the good field amplitude in V/m, which means a scale of 9.327 to have a field in MV/m which is what is expected by ASTRA. We will use the same scale factor for B, which will give us fields in MTesla, which is an non usual unit, but it seems that it is what is needed by astra. As our hfss field map represent H, we will also multiply this by
V/m, and a scale of 9.3227e+6 to have the good field amplitude in V/m, which means a scale of 9.327 to have a field in MV/m which is what is expected by ASTRA. We will use the same scale factor for B, which will give us fields in MTesla, which is an non usual unit, but it seems that it is what is needed by astra. As our hfss field map represent H, we will also multiply this by  .
.
In the previous section, we used
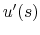
where

is the curviligne coordinate. But we can also interprete it as the angle between the U axis (X or Y axis) and the beam trajectory tangent. This makes the link between the optical example given previously and the beam dynamics section. As a result of this, as the tangent of this angle in radian is equal to the ratio between

and
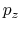
(respectively

and
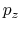
), we can write, in the approximation of small deflection around the main trajectory z axis:
 |
(14.11) |
This will be useful when we will further need to go from
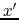
to

and

' to

.
Now that the link between

derivative, momentum and angle is made, it is time to introduce the notations for a three dimensional beam. For practical reason, as the curvilign coordinate

is really close to

along the trajectory inside the cavity, we will use

. Thus this will be the structure of the input vector for the cavity matrix, and we will pay attention to the units:
And our problem is, determining the matrix of the 5 cell cavity, assuming that it is constant if we consider beam trajectories which are really close to the reference particule. This matrix should give us the folowing relation for every input vetor
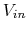
, which represents a particule a little bit offset relatively to the reference particule, and gives use all the parameters values at the en of the cavity for this same particule,
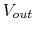
:
 and the energy
and the energy
 and the energy
and the energy

![]() is a constant for a given particle. We will thus introduced the phase
is a constant for a given particle. We will thus introduced the phase
![]() with
with
![]() . This traduce that the difference of arrival time in the cavity between the particles of the bunch can be expressed by a difference of phase in the expression of the field.
The total energy gained by a particle during its travel through the caviy is then obtained by calculating the following integreal:
. This traduce that the difference of arrival time in the cavity between the particles of the bunch can be expressed by a difference of phase in the expression of the field.
The total energy gained by a particle during its travel through the caviy is then obtained by calculating the following integreal:
![$\displaystyle \int_{z=0}^{z=l_c} \left[ \cos(\phi)-\cos({2kz+\phi}) \right]dz = \frac{1}{2k}\left[ \sin(\phi+2kl_c)-sin(\phi) \right] +l_c \cos(\phi)$](img644.gif)

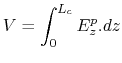
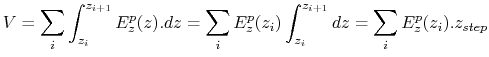
![]() V/m, and a scale of 9.3227e+6 to have the good field amplitude in V/m, which means a scale of 9.327 to have a field in MV/m which is what is expected by ASTRA. We will use the same scale factor for B, which will give us fields in MTesla, which is an non usual unit, but it seems that it is what is needed by astra. As our hfss field map represent H, we will also multiply this by
V/m, and a scale of 9.3227e+6 to have the good field amplitude in V/m, which means a scale of 9.327 to have a field in MV/m which is what is expected by ASTRA. We will use the same scale factor for B, which will give us fields in MTesla, which is an non usual unit, but it seems that it is what is needed by astra. As our hfss field map represent H, we will also multiply this by ![]() .
.
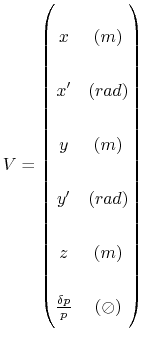
 (a)
(a)
 (b)
(b)

