Site perso : Emmanuel Branlard
- 14.2.1 Equation of motion in a pillbox
- 14.2.2 The One cell pill box model
- 14.2.3 Cavity Transit matrix
14.2 An example of transportation matrix: five cell cavity
In this part, we will modelized a five cell cavity by five pillboxes and two drifts pipe on each side of the five cells. Such a cavity is present on a0 beam line.
We will assume that the ![]() displacement isn't influenced by the cavity, which means that in this plane the beam exactly behave like in a drift. As a result of this we will work with a 4D matrix, and we will add the 2
displacement isn't influenced by the cavity, which means that in this plane the beam exactly behave like in a drift. As a result of this we will work with a 4D matrix, and we will add the 2 ![]() -components at the end of our study.
-components at the end of our study.
14.2.1 Equation of motion in a pillbox
The following calculation where developped in a similar way by Donald A. Edwards [10]. We kept harmonious notations. Here we will use the S axis, which will be identical to the Z axis. The middle of the cell will correspond to| (14.12) | |||
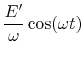 |
(14.13) |
The equations of motion, with the only Lorentz force
We will define without justification the transit time factor T:

14.2.2 The One cell pill box model
For a particle leading the reference particle by a distance z we have:
| (14.16) | |||
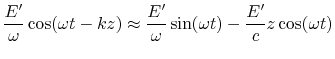 |
(14.17) |
which can be written differently using
And for a particle, set at
Substracting those two sets of equations gives us
Let's integrate 14.23 from
 |
(14.24) |
Now, as
Which we can integrate again:
The integration of 14.24 is now possible thanks to the two last expressions. We will provide details of the algebra here. Inserting expressions 14.26 and 14.27 in equation 14.24 yields to:
![$\displaystyle \frac{Tkp}{2} \left[ x_{in}+\left(x'_{in}+\frac{Tp}{2}z\right)\left(s+\frac{\lambda}{4}\right)-\frac{Tp}{2k}z\cos(ks) \right] \cos(ks)$](img708.gif) |
(14.27) | ||
![$\displaystyle \frac{Tp}{2} \left[ x'_{in}+\frac{Tp}{2}z\sin(ks)+\frac{Tp}{2}z \right] \sin(ks)$](img709.gif) |
(14.28) |
After factorization:
![$\displaystyle x_{in} \frac{T}{2}p\left[k\cos(ks)\right]$](img710.gif) |
(14.29) | ||
![$\displaystyle x'_{in} \frac{T}{2}p \left[k\left(s+\frac{\lambda}{4}\right) \cos(ks) + \sin(ks)\right ]$](img712.gif) |
(14.30) | ||
![$\displaystyle z \frac{T^2}{4}p \left[k\left(s+\frac{\lambda}{4}\right)\cos(ks)-\cos^2(ks)+\sin^2(ks)+\sin(ks)\right]$](img713.gif) |
(14.31) |
We use the relation
![]() , and the following integrals:
, and the following integrals:
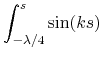 |
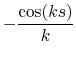 |
(14.32) | |
 |
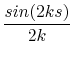 |
(14.33) | |
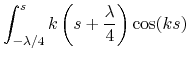 |
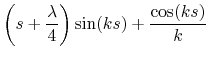 |
(14.34) |
It yields:
|
|
14.2.3 Cavity Transit matrix
To have the matrix of the entire cell we just have to evaluate the previous expression at
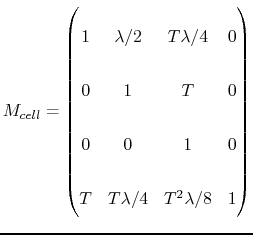
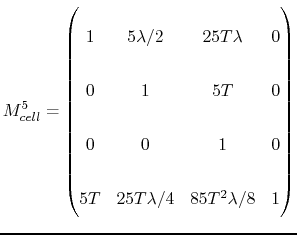
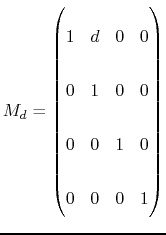
Eventually, the matrix of the whole cavity with surrounding pipes is:
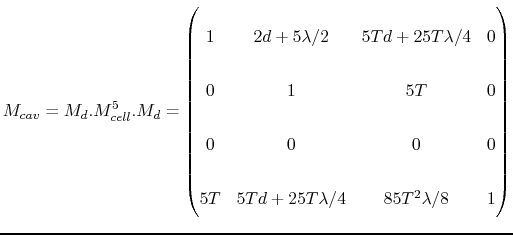

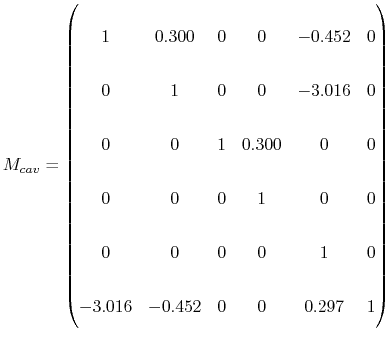
Numerically:
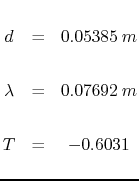
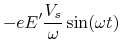
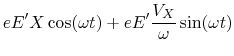
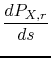
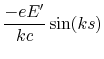
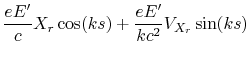
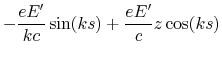

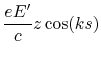
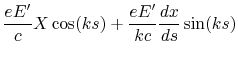
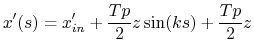
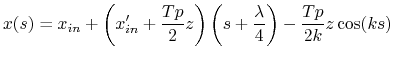
![$\displaystyle x_{in}\;\frac{T}{2}\left[1+\sin(ks)\right]$](img722.gif)
![$\displaystyle x'_{in}\;\frac{T}{2}\left[\left(s+\frac{\lambda}{4}\right)\sin(ks)\right]$](img723.gif)
![$\displaystyle z \;\frac{T^2}{4}\left[\left(s+\frac{\lambda}{4}\right)\sin(ks)-\frac{1}{2k}\sin(2ks)\right]$](img724.gif)