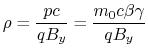Site perso : Emmanuel Branlard
Subsections
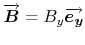 , so that the beam is deviated in the plane
, so that the beam is deviated in the plane 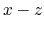 . Without electric field the equation of motion in gaussian units reduces to (equations 1.1 and 1.2):
. Without electric field the equation of motion in gaussian units reduces to (equations 1.1 and 1.2):
Projecting along the x coordinates we have :
Eventually, the radius of the trajectory can be expressed in terms of the magnetic field :
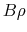 is called the magnetic rigidity.
is called the magnetic rigidity.
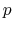 . Thus a succesion of two dipoles will transform a longitudinal spread of momentum
. Thus a succesion of two dipoles will transform a longitudinal spread of momentum 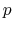 into a spread of transversal position
into a spread of transversal position 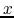 , as illustrated on figure 11.1. This principle is used for emittance exchange doglegs and compressors. The path of the particle of low momentum is longer than the one of high momentum. Thus, if the initial distribution has a negative corelation between position and energy, this correlation will be reduced as the high momentum tail will travel along a smaller distance than the head, catching up with the head of the distribution.
, as illustrated on figure 11.1. This principle is used for emittance exchange doglegs and compressors. The path of the particle of low momentum is longer than the one of high momentum. Thus, if the initial distribution has a negative corelation between position and energy, this correlation will be reduced as the high momentum tail will travel along a smaller distance than the head, catching up with the head of the distribution.
As one can see on figure 11.4, the magnetic field is not constant at the vicinity of the dipole edges. The field start dropping inside the dipole and continue to have a significant influence outside the dipole metallic frontier. This is called the fringe fields. It is commonly recognize that the fringe fields extend outside the pole tips is a function of the gap between the two pole tips. From this, several empirical models can be suggested. We will here mention the Henge's field fall off model, which can be expressed as:
where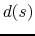 is the distance to the effective field boundary (the magnet edge),
is the distance to the effective field boundary (the magnet edge), 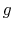 is a scaling factor of the order of the gap size which determines the fringe fields extent, and the
is a scaling factor of the order of the gap size which determines the fringe fields extent, and the 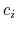 are coefficients that determines the shape of the fringe field. A reasonable value for the degree of the polynom is
are coefficients that determines the shape of the fringe field. A reasonable value for the degree of the polynom is 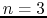 . Astra uses a polynome of degree 1. As we will further see(figure 11.7), this value should be extended in order to allow a beter fitting with the experimental data.
. Astra uses a polynome of degree 1. As we will further see(figure 11.7), this value should be extended in order to allow a beter fitting with the experimental data.
It corresponds to a abstract length of the dipole fs the field was constant equal to inside the dipole, and null outside. As we saw before, this is not likely the case, so that we will always have:
inside the dipole, and null outside. As we saw before, this is not likely the case, so that we will always have:
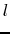 eff
eff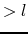 , where
, where  is the real length of the dipole.
is the real length of the dipole.
- 11.1.1 Equation of motion
- 11.1.2 Successions of dipole - reducing the energy spread
- 11.1.3 Fringe fields
- 11.1.4 Effective length
11.1 Theory
11.1.1 Equation of motion
An ideal dipole consists in a constant magnetc field of constant direction, between two metallic pole tips. The magnetic fields is produced by a coil perpendicular to the pole tips, so that the magnetic lines in the dipole are perpendicular to the two surfaces of the pole tips. In the classic coordinate system, we will have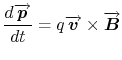 |
(11.1) |
This equation can be integrated numerically to determine the trajectory, in case of a non constant magnetic field. Nevertheless, assuming a constant magnetic field, one can show that from curvilinear coordinates we have :
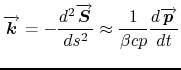 |
(11.2) |
Projecting along the x coordinates we have :
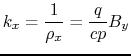 |
(11.3) |
Eventually, the radius of the trajectory can be expressed in terms of the magnetic field :
11.1.2 Successions of dipole - reducing the energy spread
From equation 11.4 one can see that the deviation introduced by a dipole depends on the momentum
11.1.3 Fringe fields
As one can see on figure 11.4, the magnetic field is not constant at the vicinity of the dipole edges. The field start dropping inside the dipole and continue to have a significant influence outside the dipole metallic frontier. This is called the fringe fields. It is commonly recognize that the fringe fields extend outside the pole tips is a function of the gap between the two pole tips. From this, several empirical models can be suggested. We will here mention the Henge's field fall off model, which can be expressed as:
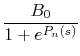 |
(11.5) | ||
 |
(11.6) |
where
11.1.4 Effective length
The effective length is defined as: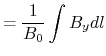 |
(11.7) |
It corresponds to a abstract length of the dipole fs the field was constant equal to